Construire des polygones réguliers
Construction avec une règle non graduée et un compas des polygones réguliers du triangle équilatéral au dodécagone régulier (12 côtés).
Le triangle équilatéral (inscrit dans un cercle donné)
Le triangle équilatéral est un polygone régulier à 3 côtés.
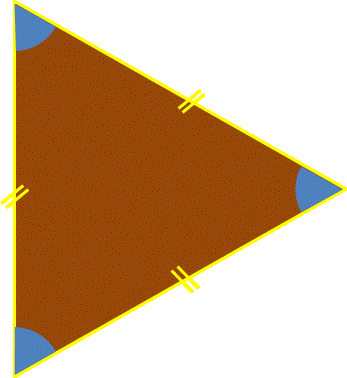

Exercice de construction sur GeoGebra : un message apparaîtra lorsque le polygone cherché sera construit (utiliser l'outil "polygone").
Le carré
Le carré est un polygone régulier à 4 côtés.


Exercice de construction sur GeoGebra : un message apparaîtra lorsque le polygone cherché sera construit (utiliser l'outil "polygone").
Le pentagone régulier
Le pentagone régulier est un polygone régulier à 5 côtés.


Exercice de construction sur GeoGebra : un message apparaîtra lorsque le polygone cherché sera construit (utiliser l'outil "polygone").
L'hexagone régulier
L'hexagone régulier est un polygone régulier à 6 côtés.


Exercice de construction sur GeoGebra : un message apparaîtra lorsque le polygone cherché sera construit (utiliser l'outil "polygone").
L'heptagone régulier (construction approchée)
L'heptagone régulier est un polygone régulier à 7 côtés.
Il n'est pas possible de le construire de façon exacte avec seulement une règle non graduée et un compas. La méthode approchée présentée ici en est une très bonne approximation.


Exercice de construction sur GeoGebra : un message apparaîtra lorsque le polygone cherché sera construit (utiliser l'outil "polygone").
L'octogone régulier
L'octogone régulier est un polygone régulier à 8 côtés.


Exercice de construction sur GeoGebra : un message apparaîtra lorsque le polygone cherché sera construit (utiliser l'outil "polygone").
Le nonagone (ennéagone) régulier (construction approchée)
Le nonagone ou ennéagone régulier est un polygone régulier à 9 côtés.
Il n'est pas possible de le construire de façon exacte avec seulement une règle non graduée et un compas. La méthode approchée présentée ici en est une très bonne approximation.


Exercice de construction sur GeoGebra : un message apparaîtra lorsque le polygone cherché sera construit (utiliser l'outil "polygone").
Le décagone régulier
Le décagone régulier est un polygone régulier à 10 côtés.


Exercice de construction sur GeoGebra : un message apparaîtra lorsque le polygone cherché sera construit (utiliser l'outil "polygone").
L'hendécagone régulier (construction approchée)
L'hendécagone régulier est un polygone régulier à 11 côtés.
Il n'est pas possible de le construire de façon exacte avec seulement une règle non graduée et un compas. La méthode approchée présentée ici en est une très bonne approximation et elle nécessite l'usage d'une équerre.


Dodécagone régulier
Le dodécagone régulier est un polygone régulier à 12 côtés.
Cette première méthode utilise l'hexagone régulier comme base de construction.

Cette seconde méthode utilise le carré comme base de construction.


